Midsized program

For my midsized program I wanted show the implementation of a couple of different sorting algorithms.

The first sorting algorithm that I would like to implement in Haskell is the quick sort algorithm. Here is a little graphic about quick sort (complements of wikipedia.org).

             
Quick sort creates a pivot point and then compares each of the other elements in the array to that value and then to the values next to them until each value is sorted (as shown above). The way I went about this was by first thinking about how I would implement the quicksort algorithm in Java and that got me started on some pseudocode. Then it was a matter of writing the algorithm in Haskell based on some of the other principles in Haskell as discussed previously in this blog.

As I discussed earlier when you make a function you need to start by giving the function a name and defining the types that it takes and returns.

qs:: (Ord i) => [i] -> [i]

In this case I called the function qs and said that it takes an Ord input (Which is Haskell speak for something that can be ordered stands for Ordering) in this case it will be a list called i and says that each element in the list will maintain the same type it initially was. Very similar to functions we have seen in the past during this blog.

Next comes the actual meat of the algorithm here is what I came up with:

qs(x:xs) = qs[y | y <- xs, y <= x] ++ [x] ++ qs[y | y <- xs, y > x]

I like to think about this in three main parts.

Part 1:

qs(x:xs)

This part takes the name of the function and says that (x:xs) meaning that an element x is compared to each of the other elements in the array, noted as xs. This is a coding standard in Haskell.

The next section:

qs[y | y <- xs, y <= x]

This part says that the remaining elements in the list being compared is now known as y and if y is less than or equal to x (the current item being compared) it should be moved over one place to the left and then the rest of the list is concatenated to the end (++[n]).

The last part is:

qs[y | y <- xs, y > x]

and this is the oppositive of the previous section. It takes all of the xs currently being compared and then moves it to the right and attaches the rest of the list to the left side.

Now since this is a recursive function (meaning it calls itself again and again until each element of the list is sorted) we must have a way to get out of the recursion otherwise we would be stuck. This is as simple as saying qs[] = [] which means it will stop when there are no more elements to be compared.

Let's take a look at the implementation:

and here is what happens when we run it:

Success!  The list has been sorted.

The next algorithm that I will take a look at will be the Bubble Sort.

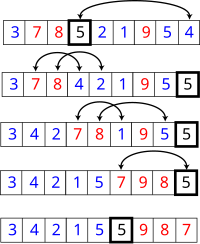
Once again here are a couple of diagrams that explain exactly what Bubble sorting is (courtesy wikipedia.org)

      

Basically the way bubble sort works is by starting at the beginning and checking to see if the first two elements are in the correct order and if they are it stays the same, if not the smaller one is swapped with the larger one. The slowly moves the largest ones to the end and the smaller ones to the beginning.

I have for another class (Bioinformatics) implemented a version of the Bubble sort algorithm in Java and so I know the general procedure for implementation however since this is Haskell I had to do a little more outside research until I was fully able to compose a working piece of code. However, I am glad I had to do some more research because that meant I learned a lot.

Previously in this blog I have talked about the map and filter functions of Haskell. I had to use something similar in this code but instead of using a map I had to use a variation of the fold method (which is a combining function) known as foldl. This tripped me up for a while because I was trying to map over the function but this was not working. I found a couple of very helpful articles on StackOverFlow that helped me understand the need for foldl vs mapping.

Once I understood a little bit more about the nuances of Haskell I was read to begin once again I started by giving the function a name and defining the types/

Like so:
bbs:: [Int] -> [Int]

This gives the function a name and says what type each element is passed in as and what the expected return should be in.

The next bit of code was:

bbs (x:xs) =  step $ foldl go (x,[]) xs where

This starts out the same way as above, comparing a piece of the list to the entire list. This is where I had to go on the Haskell documentation and look up the foldl syntax which includes the step and go syntax. This allows us to go through each element of the array next we will see how to compare them using a new function called mapAccumL or just acc as it is referenced. (documentation here: Documentation)

The next bit is the actual compasion:

go (y,acc) x = (min x y, max x y : acc)

  step (x,acc) = x : bbs acc

This took me a long time of struggling and research to come up with and I am not sure if it is the most efficient way but it seems to work! This section takes a look at each individual x and y pairing and sees if they are in the correct order. If they are it leaves it the same, if not it will reverse the order.

Let's take a look at the final implementation:

And the results:

These are the two examples I decided to explore and work with. I feel like I learned a lot and I really enjoy the syntax of this. It is very mathematical and laid out simply. It reminds me of the math logic from CS242.

Thanks for reading and bearing with the long post.

Stay tuned for more Haskell Programming