Final Haskell Project: A brief study in Parrallism

Nested List Processing

As we have learned previously in this blog, Haskell is a language where lists are very important and therefore unsurprisingly one of the most important issues that must be addressed when programming in Haskell is how exactly are operations applied to lists?

In order to see if we can find some of the issues with operations on lists, let's write a quick maximum function that takes a list and returns the max value of the list.

This is a pretty standard way to do this in Haskell, let's take a closer look about how it works.

Fist we must import the Data.List library

Next we can define a function and give it a type definition.

The first line of actual code reads: 

maximum':: (Ord a) => [a] -> a

You may remember this means we will be ordering something in this function. In this case we tell the function to take a list ([a]) and return a single value (a).

The next line simply takes the element of the list and sets it to the Lambda Variable x

Finally the line maximum' (x:xs) = max x (maximum' xs)starts at the head of the list and recursively goes through and finds the maximum value in the list.

So far this is nothing we haven't already done in this blog and so we can expect to have success in our simple maximum function. Here are a few examples:

Success!

 

And again nothing really surprising here.

So where does the problem come in? Consider this, what if we had a list of lists and I wanted to find the biggest value in the entire collection? What would I happen if I just gave our regular function a list of lists? Let's see!

So here is the same function with a list of lists being passed in, rather than a list of simple integers:

So what we would want to happen is have the function return a value of 11. This is the result when this method is run:

 

Shoot! That's not quite what we were expecting. Why was a list returned instead of a single integer? The way this method is currently written can not handle nested lists. It simply finds the list with the greatest number of elements instead of the highest value from any list. How can we modify this?

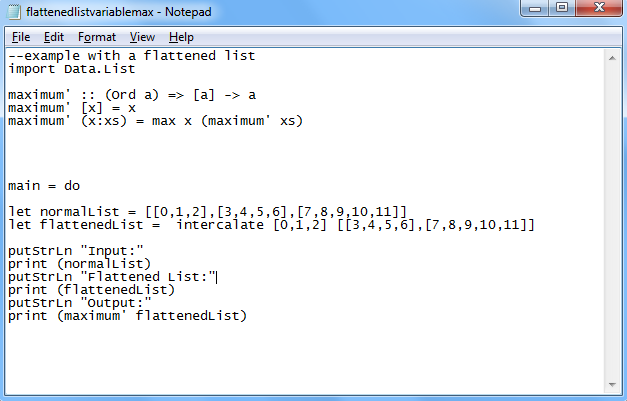
In Haskell a pretty popular way to handle these lists is to flatten them. This is done by using a method within the standard Data.List library called intercalate. This method takes a list of lists and flattens it down to one list. Here is how I decided to implement this in Haskell:

And here is the result:

 

Now we can observe the result of 11 that we might have expected from the first method. This begs the question, which is a better way to handle lists? Well that depends if you have nested list values and you want a simple maximum of any element in any list or sub-list then the method using flattening is the correct way to do it. However if you have data and you want to know which list has the most elements in it the first way with a non-flattened list of lists would be the correct approach.

This is the example I decided to look at for my final example of Haskell programming. Overall I enjoyed learning about this language even though it was far more challenging than I had anticipated. Functional programming requires a far different way of thinking than the traditional object orientated programming that I had been familiar with. It was an interesting study.

I hope you had as much fun reading this blog as I had writing it. 

That's all for now.

Haskell Week 9

Syntactic Sugar:

Syntactic sugar is a way of making code more concise which makes it easier to not only write but also easier to read. 

Haskell is notorious for using these little short cuts to make bulky code "sweeter" and easier to understand. For example in a number of examples in this blog the syntax I used was the syntactic sugar equivalent for longer less attractive code.

Here is one example of a map that we looked at earlier in this blog



As you can see I used a map to add one to each of the Integers in the list [1,3,5,7,9] thanks to the magic of syntactic sugar I was able to simply say map (+1) and it knew exactly what I was talking about. The way Haskell can do this is by taking my "sweet" version of syntax and converting it back to the clunky unappealing code. In this case map (+1) translates to \x -> x + 1 which simply makes a lambda and assigns it to the value of x +1.

Another "sweet" piece of syntax in the same example is the list itself. To make the list I simply put the numbers I want to be members and they are added to a new list. Magic right? Wrong! Syntactic sugar! Once again Haskell interpreted my list as (:) 1 ((:) 3 ((:) 5 ((:) 7 ((:) 9 [])) This is the longhand way of creating a list, it uses cons (constructors (NOT LIKE IN JAVA)) to add each element to an empty list until the list is no longer empty.

Other shortcuts (Most of which I have used):

You can let Haskell do a lot of the work for you specifically with sequences. If I were to write print ([1..4]) Haskell would know to return 1,2,3,4 because I set a start point (1) and an end point (4) it then understand the ".." to mean "fill in the blanks here" The longer way to do this would be to use the built in function called enumFromTo and call it on the tuple 1, 5 like so: enumFromTo 1 5.

Even such things as if-else blocks (which really uses cases) are generally written in the short hand. Which I find to be an okay way to do it as long as there is an understanding of the "unsweet" code behind the abbreviations.

Haskell Week 8

Exceptions:

Exceptions and the way we handle them in Haskell are very similar to the methods we use in Java. Exceptions can be thrown, caught, and handled.

Some of the most common exceptions in Haskell include:

isAlreadyExistsError
isDoesNotExistError
isAlreadyInUseError
isFullError
isEOFError
isIllegalOperation
isPermissionError
isUserError

I find that the error reporting is much more readable and helpful in Haskell then in some of the other languages we have looked at, such as Java, VB, C#, and Python.

Here is a little error that I was given when I tried to run a method without creating an instance of anything to be returned to the console:

<interactive>:22:1:

    No instance for (Fractional [t0]) arising from a use of `myDiv1'

    Possible fix: add an instance declaration for (Fractional [t0])

    In the expression: myDiv1 50 [1, 2, 5, 0, ....]

    In an equation for `it': it = myDiv1 50 [1, 2, 5, ....]

<interactive>:22:8:

    No instance for (Num [t0]) arising from the literal `50'

    Possible fix: add an instance declaration for (Num [t0])

    In the first argument of `myDiv1', namely `50'

    In the expression: myDiv1 50 [1, 2, 5, 0, ....]

    In an equation for `it': it = myDiv1 50 [1, 2, 5, ....]

<interactive>:22:12:

    No instance for (Num t0) arising from the literal `1'

    The type variable `t0' is ambiguous

    Possible fix: add a type signature that fixes these type variable(s)

    Note: there are several potential instances:

      instance Num Double -- Defined in `GHC.Float'

      instance Num Float -- Defined in `GHC.Float'

      instance Integral a => Num (GHC.Real.Ratio a)

        -- Defined in `GHC.Real'

      ...plus three others

    In the expression: 1

    In the second argument of `myDiv1', namely `[1, 2, 5, 0, ....]'

    In the expression: myDiv1 50 [1, 2, 5, 0, ....]

Not only is the error shown, but there are also possible solutions that are given to attempt to correct the error. I have found that these solutions are actually very helpful and often times lead to fixing the problem and producing working code.

Haskell Week 7

Concurrency vs Parallelism

According to the Haskell Documentation there is a distinct difference between concurrency and parallelism.


Parallelism is "a technique to make programs faster by performing several computations in parallel. This requires hardware with multiple processing units" (Haskell)

Whereas, concurrency "refers to techniques that make program more usable. Concurrency can be implemented and is used a lot on single processing units, nonetheless it may benefit from multiple processing units with respect to speed". (Haskell)

So what exactly is the difference?

According to Simon Mar, in his blog ghcmutterings, "a concurrent program is one with multiple threads of control" all of which operate on one processor and share that processors resources.

This leads to the question what is a thread?

Threads are contained inside of processes a process can have multiple threads all of which share the processes resources, but they are also able to accomplish goals individually. An application may have multiple processes, and these processes may spin up multiple threads. The key to this is they all happen on one processor.

The key distinguishing factor with parallel processing is that more than one CPU is needed.

There has been an extensive amount of research as to the benefits of parallelism.

I found Simon Mar's research to be very helpful in trying to understand this very complex and high level issue

http://community.haskell.org/~simonmar/par-tutorial.pdf    

Midsized program

For my midsized program I wanted show the implementation of a couple of different sorting algorithms.

The first sorting algorithm that I would like to implement in Haskell is the quick sort algorithm. Here is a little graphic about quick sort (complements of wikipedia.org).

             
Quick sort creates a pivot point and then compares each of the other elements in the array to that value and then to the values next to them until each value is sorted (as shown above). The way I went about this was by first thinking about how I would implement the quicksort algorithm in Java and that got me started on some pseudocode. Then it was a matter of writing the algorithm in Haskell based on some of the other principles in Haskell as discussed previously in this blog.

As I discussed earlier when you make a function you need to start by giving the function a name and defining the types that it takes and returns.

qs:: (Ord i) => [i] -> [i]

In this case I called the function qs and said that it takes an Ord input (Which is Haskell speak for something that can be ordered stands for Ordering) in this case it will be a list called i and says that each element in the list will maintain the same type it initially was. Very similar to functions we have seen in the past during this blog.

Next comes the actual meat of the algorithm here is what I came up with:

qs(x:xs) = qs[y | y <- xs, y <= x] ++ [x] ++ qs[y | y <- xs, y > x]

I like to think about this in three main parts.

Part 1:

qs(x:xs)

This part takes the name of the function and says that (x:xs) meaning that an element x is compared to each of the other elements in the array, noted as xs. This is a coding standard in Haskell.

The next section:

qs[y | y <- xs, y <= x]

This part says that the remaining elements in the list being compared is now known as y and if y is less than or equal to x (the current item being compared) it should be moved over one place to the left and then the rest of the list is concatenated to the end (++[n]).

The last part is:

qs[y | y <- xs, y > x]

and this is the oppositive of the previous section. It takes all of the xs currently being compared and then moves it to the right and attaches the rest of the list to the left side.

Now since this is a recursive function (meaning it calls itself again and again until each element of the list is sorted) we must have a way to get out of the recursion otherwise we would be stuck. This is as simple as saying qs[] = [] which means it will stop when there are no more elements to be compared.

Let's take a look at the implementation:

and here is what happens when we run it:

Success!  The list has been sorted.

The next algorithm that I will take a look at will be the Bubble Sort.

Once again here are a couple of diagrams that explain exactly what Bubble sorting is (courtesy wikipedia.org)

      

Basically the way bubble sort works is by starting at the beginning and checking to see if the first two elements are in the correct order and if they are it stays the same, if not the smaller one is swapped with the larger one. The slowly moves the largest ones to the end and the smaller ones to the beginning.

I have for another class (Bioinformatics) implemented a version of the Bubble sort algorithm in Java and so I know the general procedure for implementation however since this is Haskell I had to do a little more outside research until I was fully able to compose a working piece of code. However, I am glad I had to do some more research because that meant I learned a lot.

Previously in this blog I have talked about the map and filter functions of Haskell. I had to use something similar in this code but instead of using a map I had to use a variation of the fold method (which is a combining function) known as foldl. This tripped me up for a while because I was trying to map over the function but this was not working. I found a couple of very helpful articles on StackOverFlow that helped me understand the need for foldl vs mapping.

Once I understood a little bit more about the nuances of Haskell I was read to begin once again I started by giving the function a name and defining the types/

Like so:
bbs:: [Int] -> [Int]

This gives the function a name and says what type each element is passed in as and what the expected return should be in.

The next bit of code was:

bbs (x:xs) =  step $ foldl go (x,[]) xs where

This starts out the same way as above, comparing a piece of the list to the entire list. This is where I had to go on the Haskell documentation and look up the foldl syntax which includes the step and go syntax. This allows us to go through each element of the array next we will see how to compare them using a new function called mapAccumL or just acc as it is referenced. (documentation here: Documentation)

The next bit is the actual compasion:

go (y,acc) x = (min x y, max x y : acc)

  step (x,acc) = x : bbs acc

This took me a long time of struggling and research to come up with and I am not sure if it is the most efficient way but it seems to work! This section takes a look at each individual x and y pairing and sees if they are in the correct order. If they are it leaves it the same, if not it will reverse the order.

Let's take a look at the final implementation:

And the results:

These are the two examples I decided to explore and work with. I feel like I learned a lot and I really enjoy the syntax of this. It is very mathematical and laid out simply. It reminds me of the math logic from CS242.

Thanks for reading and bearing with the long post.

Stay tuned for more Haskell Programming 

Haskell week 6

This week my main focus was on exploring some of the more useful libraries in Haskell I was amazed at how many cool features there are in some of these libraries. I explored a couple of different libraries so this post is going to be somewhat varied topic wise, but I think it is worth knowing some of these odds and ends of Haskell.

 Data.List

I researched some Haskell documentation and decided to test a couple of the functions that fall under the Data.List library.

Let's take a look at a little section of code I wrote:

The first thing that we have to do is import the Data.List library (this is done in a similar way to java). Once we have the library imported we can begin to use the methods it contains. The next line of code defines the main function of the program and the "do" command lets us erm, well... it let's us do things (like printing). The first method is the concat method. It takes the given strings and concatenate them together in the order they were given. Next we use the intersperse method which takes two parameters a character and then a string. The first character is placed between each character in the second parameter. Next we use the sort feature (pay special attention to this!). Lastly, we use the sub-sequences method which takes a string and returns a list of the possible substrings.

Let's take a look at the outputs:

Are these the results we would expect? I think so!

 System.CPUTime

The CPUTime library has two methods that are associated with it. The first is getCPUTime which returns the number of  picoseconds of CPU time that are currently being used by the program. I think this is a very interesting feature of Haskell. The second method is the cpuTimePrecision which is the smallest measurable difference in CPU time that the implementation can record. 


Let's take a look at the implementation:

And now the results:

Very cool!

Data.Char
The next Library that I looked at was Data.Char this library has some pretty standard methods but they still can be very useful. It has the standard methods such as isAlpha which returns a Boolean, isDigit, also a Boolean and some other built in ones such as digitToInt and intToDigit.

Let's take a look:

And the results:

Although this might seem somewhat trivial it will become important when we move on to other concepts.

Data.Tree

I decided to take a look at the Data.Tree library because in many of my CS classes I keep hearing about Trees so I wanted to do a little bit of research and make a couple of trees in Haskell.

and here you can see a visual:

Just a surface level example of trees.

That is it for now. Stay tuned for my progress with Haskell.

Haskell Week 5

This week I have not made as must progress in the past with Haskell due mainly to studying for finals.

However, I did take the time to investigate some of the real world applications of the language.

It seems from my research that applications of  Haskell are mainly academic based. But some large companies such as Facebook and Google report that some of their in house tools are written in Haskell. Also a large banking company uses Haskell for some of their security features.

I was very interested in the security applications of Haskell but I was unable to find very much detail, perhaps unsurprisingly.